考研考数学的小伙伴都知道二元隐函数求极值是一个计算量巨大的问题，那么怎么快速又简洁地计算出来，以下题为例。

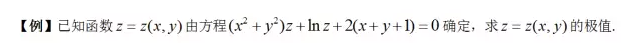
　　大家知道，求二元函数极值的步骤：
　　1.找驻点；
　　2.分别求驻点处A,B,C；
　　3.求出极值。
　　但这类问题，第一步驻点就会遇到麻烦，涉及到二元隐函数方程求偏导，这里我们一般有两种方法。
　　一、直接对方程两边分别关于变量x,y求导，z看作x,y的函数；
　　二、隐函数存在定理，也即公式法计算一阶偏导数。
　　为了后续计算方便，建议大家用第一种方法求导，同时令一阶偏导数为0，可以直接找出驻点。

　　接下来的工作，就需要求二阶偏导，但注意到我们只要找出ABC就够了，不需要具体的二阶偏导函数，所以接下来的步骤：

　　此时，若去求二阶偏导函数工程巨大，因为这道题会浪费掉大量的时间，你成功掉入出题人的陷进。
　　涉及到隐函数求二阶导问题，不论一元函数还是二元函数，基本都只考它们在一点处取值，只需：求而不解，代入法就能轻松化解计算量巨大的尴尬，你们，GET到了吗？
　　解答：